THEORETICAL PHYSICIST
Racah Institute of Physics, Hebrew University of Jerusalem
Erez Zohar
RESEARCH
We aim at designing new tools, methods and approaches for solving difficult problems in many-body physics. On the process, we get to reconstruct physical models out of elementary ingredients (such as in the construction of tensor network states) or different building blocks (as in the design of a quantum simulator). In the process of reconstructing a theory from scratch, we get to learn a lot about it, to see it from new perspectives, to understand it better and to take it to new directions.
Tensor Network approaches to quantum field theory and many body physics
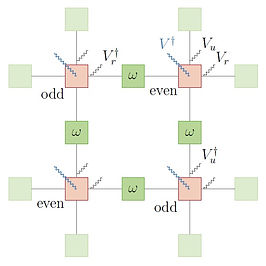
Lecture Notes:
Emonts, P. and Zohar, E., Gauss law, Minimal Coupling and Fermionic PEPS for Lattice Gauge Theories, SciPost Phys. Lect. Notes 12 (2020)
The physical properties of strongly correlated many body systems heavily depend on their entanglement structure – nontrivial quantum correlations that do not allow one to use semi-classical or perturbative approaches. Quantum information studies of entanglement theory have brought us now to a point in which entanglement can be studied, quantified and manipulated, allowing us to use it as a resource for studying many body physics.
Tensor network states form a special class of quantum many body states, constructed from local building blocks (tensors) in a way that gives rise to the right entanglement structure of "physically relevant" states of such systems (e.g. ground states and first excited states of local Hamiltonians). They allow one to encode symmetries easily on the local level and parameterize states invariant under arbitrary symmetry groups; and depend on a small number of parameters. All these, combined with analytical and numerical tools, make them excellent ansatz states for many body theories.
I am interested in the use of tensor network states for studying gauge theories and high energy physics in general. I have been one of the first to extend the formalism of globally invariant PEPS (Projected Entangled Pair States – a particular tensor network construction) to states with gauge symmetries, and the first to construct tensor network states with fermionic matter and quantum gauge fields. I have introduced a method that combines tensor networks with Monte-Carlo computations, allowing one to perform efficient numerical computations with tensor networks for gauge theories in more than one space dimension.
On the right: a talk titled "Gauged gaussian fermionic PEPS" given at the online seminar series on Tensor Networks in High Energy Physics, MPI for Gravitation, Potsdam, December 2021.
On the right: a talk given at the Workshop Tensor Networks: from Simulation to Holography II at DESY, Zeuthen, Germany, in March 2019.

Quantum field theory is the mathematical language in which quantum many body theories are usually formulated. It is equipped with several great tools for computations in the weakly interacting cases, such as perturbation theory or mean field approaches. However, when the interaction is strong, these methods fail and one has to develop and apply non-perturbative methods.
One approach that was originally suggested by Richard Feynman and has recently been applied widely, mostly for condensed matter physics, is quantum simulation, in which one maps the degrees of freedom of an inaccessible quantum system (for example, a strongly interacting one) to those of one that could be controlled and studied in the lab; this is a quantum simulator, whose study corresponds to this of the original one.
While quantum simulators have been applied mostly to condensed matter models, using atomic, optical and solid state device, I have been a part of the effort to extend quantum simulation to particle physics too, and in particular to gauge theories. I am interested in mapping between high energy models (such as QED and QCD) to atomic, optical and solid state systems, which could be used as their quantum simulators. My contributions to the field include various simulation schemes for various models using different systems, starting from the first proposal for a quantum simulation of two dimensional lattice QED, and ranging to various proposals for abelian and non-abelian gauge theories, with and without dynamical fermionic matter.
Quantum Simulation of quantum field theory and high energy physics
Scientific Reviews:
Zohar, E., Quantum Simulation of Lattice Gauge Theories in more than One Space Dimension - Requirements, Challenges, Methods, Phil. Trans. R. Soc. A 380, 20210069 (2021)
Zohar, E., Cirac, J.I. and Reznik, B., Quantum Simulations of Lattice Gauge Theories using Ultracold Atoms in Optical Lattices, Rep. Prog. Phys. 79, 014401 (2016)
Broad Audience Review:
Zohar, E., Quantum Simulation of Fundamental Physics, Nature (News and Views) 534, 480 (2016)
On the right: a talk given at the Workshop Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory, and Holography at the International Centre for Theoretical Sciences, Bangalore, India, September 2022.
Other Research Interests
Quantum Field Theories
Lattice Gauge Theories
Fermionic Physics
Formalism of Quantum Mechanics
Mathematical Physics